Sound is measured in units called decibels (dB). The higher the decibel level, the louder the noise. On the decibel scale, the level increase of 10 means that a sound is actually 10 times more intense, or powerful. Decibel Meter, TACKLIFE Digital Sound Level Meter 30-130dB (A) Range with Sound Simulation, Max/Min/Data Hold, Fast/Slow Mode, Self-Calibration Noise Meter, Battery Included -MLM02. 4.4 out of 5 stars. Decibel scores every online customer experience to expose what’s really happening on your website, and provides the most advanced tools available to understand why. A decibel (dB) is a unit of measurement for sound. A-weighted decibels, abbreviated dBA, are an expression of the relative loudness of sounds in air as perceived by our ears. SAFE & UNSAFE DECIBELS The National Institute of Occupational Safety (NIOSH) states that for a 115 decibel (dB) sound, the exposure limit is just 28 seconds.
A decibel (or dB) measures ratios of power or intensity. It expresses them as an exponential function. One bel is a power ratio of 10:1, and is divided into ten decibels. An increase of three decibels is approximately a doubling of power. Decibels are often used in measuring telecommunication signals. With electric audio signals, there are several decibel units, relative to several bases. For example, dBm is relative to one milliwatt.
It's been said that the smallest difference humans can hear is 0 dB and is related to the Absolute threshold of hearing, although this is very subjective at best.
History[change | change source]
The bel unit was named after Alexander Graham Bell. This unit was so rough that it is more typical to use the decibel, which is one bel divided by ten. Before bels, there was the Transmission Unit (TU).
Examples and Protection[change | change source]
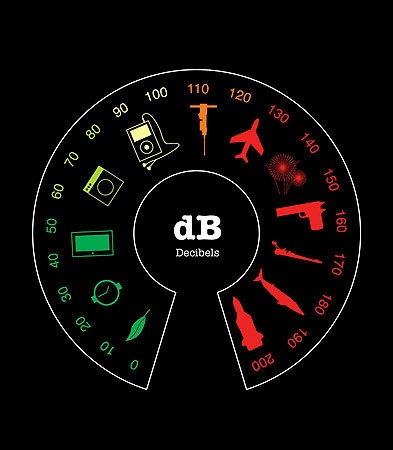
Often, decibels are used to say how loud a sound is relative to the threshold of hearing. The decibel is not an SI unit. The table here uses dBSPL as units of sound to indicate consensus on hearing protection. Some examples of sounds are:
| Sound Level | Examples |
|---|---|
| 171 dB | Next to a loud rifle being shot |
| 150 dB | Right next to a jet engine |
| 110-140 dB | Jet engine at 100 meters |
| 130-140 dB | Where most people begin to feel pain |
| 130 dB | Trumpet (a half meter in front of) |
| 120 dB | Vuvuzela horn (1 meter in front of), risk of immediate hearing loss |
| 110 dB | Gas chainsaw |
| 100 dB | Jack hammer |
| 80-90 dB | Traffic on a busy roadway |
| 60-80 dB | Passenger car |
| 40-60 dB | Normal conversation |
| 20-30 dB | Very calm room |
| 10 dB | Light leaf rustling, calm breathing |
| 0 dB | Hearing threshold right next to ear |
Hearing protection can also be used to shield from ear damage. This table gives some safe limits for the level of sound so that the ears are not damaged.
| Decibels | Maximum Exposure Time |
|---|---|
| 90 | 8 hours |
| 92 | 6 hours |
| 95 | 4 hours |
| 97 | 3 hours |
| 100 | 2 hours |
| 102 | 90 minutes |
| 105 | 60 minutes |
| 110 | 30 minutes |
| 115 | 10–15 minutes |
| 120 | 3–5 minutes |
References[change | change source]
- Plane waves
- Amplitude and intensity
- The speed of sound
- Circular and spherical waves
- Attenuation
- Impedance
- Interference
- Moving sources and observers
- Standing waves
- In stretched strings
- In air columns
- In nonharmonic systems
- Steady-state waves
- Spectral analysis
- Generation by musical instruments
- Hearing
The ear mechanism is able to respond to both very small and very large pressure waves by virtue of being nonlinear; that is, it responds much more efficiently to sounds of very small amplitude than to sounds of very large amplitude. Because of the enormous nonlinearity of the ear in sensing pressure waves, a nonlinear scale is convenient in describing the intensity of sound waves. Such a scale is provided by the sound intensity level, or decibel level, of a sound wave, which is defined by the equation
Here L represents decibels, which correspond to an arbitrary sound wave of intensity I, measured in watts per square metre. The reference intensity I0, corresponding to a level of 0 decibels, is approximately the intensity of a wave of 1,000 hertzfrequency at the threshold of hearing—about 10-12 watt per square metre. Because the decibel scale mirrors the function of the ear more accurately than a linear scale, it has several advantages in practical use; these are discussed in Hearing, below.
A fundamental feature of this type of logarithmic scale is that each unit of increase in the decibel scale corresponds to an increase in absolute intensity by a constant multiplicative factor. Thus, an increase in absolute intensity from 10-12 to 10-11 watt per square metre corresponds to an increase of 10 decibels, as does an increase from 10-1 to 1 watt per square metre. The correlation between the absolute intensity of a sound wave and its decibel level is shown in Table 1, along with examples of sounds at each level. When the defining level of 0 decibel (10-12 watt per square metre) is taken to be at the threshold of hearing for a sound wave with a frequency of 1,000 hertz, then 130 decibels (10 watts per square metre) corresponds to the threshold of feeling, or the threshold of pain. (Sometimes the threshold of pain is given as 120 decibels, or 1 watt per square metre.)
| decibels | intensity* | type of sound |
|---|---|---|
| *In watts per square metre. | ||
| 130 | 10 | artillery fire at close proximity (threshold of pain) |
| 120 | 1 | amplified rock music; near jet engine |
| 110 | 10−1 | loud orchestral music, in audience |
| 100 | 10−2 | electric saw |
| 90 | 10−3 | bus or truck interior |
| 80 | 10−4 | automobile interior |
| 70 | 10−5 | average street noise; loud telephone bell |
| 60 | 10−6 | normal conversation; business office |
| 50 | 10−7 | restaurant; private office |
| 40 | 10−8 | quiet room in home |
| 30 | 10−9 | quiet lecture hall; bedroom |
| 20 | 10−10 | radio, television, or recording studio |
| 10 | 10−11 | soundproof room |
| 0 | 10−12 | absolute silence (threshold of hearing) |
Adobe drm download mac. Although the decibel scale is nonlinear, it is directly measurable, and sound-level meters are available for that purpose. Sound levels for audio systems, architectural acoustics, and other industrial applications are most often quoted in decibels.
The speed of sound
In gases
For longitudinal waves such as sound, wave velocity is in general given as the square root of the ratio of the elastic modulus of the medium (that is, the ability of the medium to be compressed by an external force) to its density:
Here ρ is the density and B the bulk modulus (the ratio of the applied pressure to the change in volume per unit volume of the medium). In gas mediums this equation is modified towhere K is the compressibility of the gas. Compressibility (K) is the reciprocal of the bulk modulus (B), as in
Using the appropriate gas laws, wave velocity can be calculated in two ways, in relation to pressure or in relation to temperature:or
Here p is the equilibrium pressure of the gas in pascals, ρ is its equilibrium density in kilograms per cubic metre at pressure p, θ is absolute temperature in kelvins, R is the gas constant per mole, M is the molecular weight of the gas, and γ is the ratio of the specific heat at a constant pressure to the specific heat at a constant volume, Alchemy mac download.
Values for γ for various gases are given in many physics textbooks and reference works. The speed of sound in several different gases, including air, is given in Table 2.
| gas | speed | |
|---|---|---|
| metres/second | feet/second | |
| helium, at 0 °C (32 °F) | 965 | 3,165 |
| nitrogen, at 0 °C | 334 | 1,096 |
| oxygen, at 0 °C | 316 | 1,036 |
| carbon dioxide, at 0 °C | 259 | 850 |
| air, dry, at 0 °C | 331.29 | 1,086 |
| steam, at 134 °C (273 °F) | 494 | 1,620 |
Equation (10) states that the speed of sound depends only on absolute temperature and not on pressure, since, if the gas behaves as an ideal gas, then its pressure and density, as shown in equation (9), will be proportional. This means that the speed of sound does not change between locations at sea level and high in the mountains and that the pitch of wind instruments at the same temperature is the same anywhere. In addition, both equations (9) and (10) are independent of frequency, indicating that the speed of sound is in fact the same at all frequencies—that is, there is no dispersion of a sound wave as it propagates through air. One assumption here is that the gas behaves as an ideal gas. However, gases at very high pressures no longer behave like an ideal gas, and this results in some absorption and dispersion. In such cases equations (9) and (10) must be modified, as they are in advanced books on the subject.
In liquids
Decibel Chart
For a liquid medium, the appropriate modulus is the bulk modulus, so that the speed of sound is equal to the square root of the ratio of the bulk modulus (B) to the equilibrium density (ρ), as shown in equation (6) above. The speed of sound in liquids under various conditions is given in Table 3. The speed of sound in liquids varies slightly with temperature—a variation that is accounted for by empirical corrections to equation (6), as is indicated in the values given for water in Table 3.
| liquid | speed | |
|---|---|---|
| metres/second | feet/second | |
| pure water, at 0 °C (32 °F) | 1,402.3 | 4,600 |
| pure water, at 30 °C (86 °F) | 1,509.0 | 4,950 |
| pure water, at 50 °C (122 °F) | 1,542.5 | 5,060 |
| pure water, at 70 °C (158 °F) | 1,554.7 | 5,100 |
| pure water, at 100 °C (212 °F) | 1,543.0 | 5,061 |
| salt water, at 0 °C | 1,449.4 | 4,754 |
| salt water, at 30 °C | 1,546.2 | 5,072 |
| methyl alcohol, at 20 °C (68 °F) | 1,121.2 | 3,678 |
| mercury, at 20 °C | 1,451.0 | 4,760 |
In solids
For a long, thin solid the appropriate modulus is the Young’s, or stretching, modulus (the ratio of the applied stretching force per unit area of the solid to the resulting change in length per unit length; named for the English physicist and physician Thomas Young). The speed of sound, therefore, iswhere Y is the Young’s modulus and ρ is the density. Table 4 gives the speed of sound in representative solids.
| solid | speed | |
|---|---|---|
| metres/second | feet/second | |
| aluminum, rolled | 5,000 | 16,500 |
| copper, rolled | 3,750 | 12,375 |
| iron, cast | 4,480 | 14,784 |
| lead | 1,210 | 3,993 |
| Pyrex™ | 5,170 | 17,061 |
| Lucite™ | 1,840 | 6,072 |
Decibel Therapeutics
In the case of a three-dimensional solid, in which the wave is traveling outward in spherical waves, the above expression becomes more complicated. Both the shear modulus, represented by η, and the bulk modulus B play a role in the elasticity of the medium:
